A forma de representar e manipular informação está directamente relacionada com a entidade ou aparelho que o faz. Por exemplo, uma entidade biológica representa a sua informação genética através de cromossomas, que se resumem a cadeias complexas de elementos químicos. Por outro lado, uma máquina de lavar, por exemplo, representa o seu programa de lavagens por circuitos eléctricos e/ou mecanismos mecânicos. Outro tipo de aparelho vulgarmente designado por computadores caracteriza-se pelo seu funcionamento baseado em princípios lógicos e matemáticos e que vulgarmente se enuncia como sendo computadores digitais. Importa portanto distinguir dois termos Digital, e o seu oposto, Analógico.
Digital: Um sinal digital tem como característica fundamental a sua variação
por saltos numa forma descontínua e tomar apenas determinado número de valores. A sua
evolução no tempo consiste em saltar bruscamente duns valores para outros (Figura 1a);
Analógico: Pelo contrário, a característica essencial dum sinal analógico ou da
forma de onda analógica é a sua variação contínua ao longo do tempo (Figura
1b). É o que acontece no sinal de vídeo, microfone, etc. em que o sinal evolui
duma forma contínua, por vezes com variações rápidas mas "sem saltos
bruscos".
Figura 1a - Sinal digital |
Figura 1b - Sinal analógico |
Saliente-se o facto do sinal digital ser representado através dum determinado
número de valores, porventura limitado.
Uma vez que os computadores digitais comuns usam dois valores ou níveis de tensão, a sua
denominação correcta é computadores digitais binários.
A tensão desses dois níveis varia de computador para computador ou aparelho, mas em computadores e em particular no CPU, são tipicamente de 0 e 5V, 0 e 3V. Há várias razões para a utilização destes tipos de computadores, sobretudo razões tecnológicas relacionadas com os componentes electrónicos usados na sua implementação (resistências e transístores):
Figura 2a - Sinal digital binário real |
Figura 2b - Sinal digital binário conceptual |
Assim, qualquer que seja o valor representado por computadores digitais binários, este é representado por uma sequência de sinais digitais binários, ou seja através de apenas dois valores diferentes. Sob um ponto de vista de formalização e por uma atitude prática, a estes dois valores são atribuídos significados opostos tal como cheio/vazio, existente/inexistente, ligado/desligado, verdadeiro/falso, 0/1.
Mas como poderá ser representada informação tão complexa como texto, imagens, cor, som, etc. numa forma tão simples? Usando o mesmo princípio que se usa por exemplo numa linguagem moderna, agrupando símbolos básicos como as letras e símbolos dum alfabeto. Por exemplo o alfabeto português dispõe tradicionalmente de 24/26 letras mais uns tantos símbolos como acentos e pontuação. No entanto, usando estes símbolos e regras de manipulação (gramática) é possível escrever textos tão complexos como os Lusíadas (ou imagine-se, este texto...).O mesmo se passa com a matemática ou a álgebra, que tem alfabeto e simbologia própria mas que usa um conjunto de símbolos básicos e muito limitado.
Usando apenas dois valores distintos, o princípio terá de ser forçosamente o mesmo, ou seja, combiná-los em sequências representativas de dados e informação usando regras da linguagem ou da área de aplicação. Para isso é necessário:
Existem muitíssimas regras de utilização do sinal, no entanto, a divisão da
sequência de sinais binários é porventura a que mais importância apresenta.
Desde "sempre" que o Byte é a unidade de agregação
(e
separação) de dígitos binários (binary digit - bit). Um
byte é a agregação de 8 bits. Aparentemente não há nenhuma (fundamental) razão para
ser oito (porque é que se contam ovos às dúzias), mas a verdade é que desde há muito
tempo que grande parte das quantificações de informação em informática são feitas em
número de bytes.
Uma outra forma de denominar grupos de 8 bits é octeto (em francês é a denominação corrente, mas existe noutros idiomas incluindo o inglês). Para além disso, não se conhece claramente a origem do termo byte, embora se considere que foi o Dr. Werner Buchholz, gestor de projecto da IBM, que o tenha usado pela primeira vez em 1956. Talvez à escolha não seja alheio o aspecto da figura que se costuma usar para representar (Figura 3) um byte (mordida).
![]()
Figura 3 - Representação das posições dos dígitos dum byte
O termo bit é abreviado por b, enquanto byte é abreviado por B.
A quantificação em termos de bits é geralmente usada em comunicações série (bit a
bit), enquanto byte se utiliza fundamentalmente em quantidades de informação armazenada
mas também em comunicações paralelas (conjunto de bits em simultâneo).
Apresentam-se de seguida algumas unidades utilizadas para quantificar grupos de
informação binária, o que significa que tanto pode ser utilizada para bits como bytes.
Name abbrev Size ---- ------ ---- Kilo K 2^10 = 1 024 Mega M 2^20 = 1 048 576 Giga G 2^30 = 1 073 741 824 Tera T 2^40 = 1 099 511 627 776 Peta P 2^50 = 1 125 899 906 842 624 Exa E 2^60 = 1 152 921 504 606 846 976 Zetta Z 2^70 = 1 180 591 620 717 411 303 424 Yotta Y 2^80 = 1 208 925 819 614 629 174 706 176
A ANSI (American National Standard Institute) desenvolveu o ASCII (American Standard
Code for Information Interchange) e que corresponde (sucintamente) a uma tabela que
relaciona símbolos com números.
Originalmente esta tabela relacionava 127 (27) símbolos e códigos, mas
posteriormente passou a relacionar 256 (28) símbolos. Esta alteração está
relacionada com o conceito e extensão de Byte, pois se o CPU tinha capacidade múltipla
de Byte, porque "perder" um bit em cada símbolo que se trasaccionasse? Foram
então criadas extensões à tabela original, sendo que estas são normalmente utilizadas
para caracteres específicos da linguagens de cada país, nomeadamente letras com acentos
e outros símbolos específicos.
Como já se referiu, qualquer que seja o valor representado em computadores, este é representado por uma sequência de sinais digitais binários. Portanto, cada sinal de uma sequência, poderá no máximo representar dois valores.
VFFFVVVFFVVVVVVFF
10001110011111100
Se adaptarmos este tipo de representação à descrição de valores numéricos,
então, para cada dígito (sinal na sequência) temos apenas dois valores possíveis: 0 ou
1. Se desejarmos representar números superiores a 1 temos que utilizar o mesmo
procedimento que utilizamos por exemplo na base decimal, que é a base em que cada dígito
pode ter 10 valores diferentes (0-9).
A representação dos números, analisada sob o ponto de vista do incremento de uma unidade ao número
anterior, segue o princípio de que assim que determinado dígito atinge o seu valor
máximo, adiciona-se uma unidade ao dígito seguinte e o próprio dígito volta a zero. O
procedimento é o mesmo seja qual for a base numérica.
Apesar do procedimento ser o mesmo para qualquer base, aquelas que mais se usam são:
| Base Decimal (10) | Base Binária (2) | Base Octal (8) | Base Hexadecimal (16) |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 . . |
0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 10001 10010 10011 10100 10101 10110 10111 11000 11001 11010 11011 11100 . . |
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21 22 23 24 25 26 27 30 31 32 33 34 . . |
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C . . |
Tabela 1 - Relação entre as quatro base numéricas mais utilizadas
Seja qual for a base numérica, cada dígito representa um valor absoluto. Por exemplo, os mesmos dígitos têm valores diferentes consoante a base em que o número é representado:
Decimal |
Binário |
Octal |
Hexadecimal |
101(10) = 1*100+1*101+1*102 = 1 + 0 + 100 = 101(10) |
101(2) = 1*20+0*21+1*22 = 1 + 0 + 4 = 5(10) |
101(8) = 1*80+0*81+1*82 = 1 + 0 + 64 = 65(10) |
101(16) = 1*160+0*161+1*162 = 1 + 0 + 256 = 257(10) |
Ou seja, cada dígito representa em absoluto, o seu valor multiplicado pelo peso da posição que ocupa no número. Na base decimal, o primeiro dígito é o das unidades (100), o segundo representa as dezenas (101), o terceiro representa as centenas (102), etc. Na base decimal, o princípio é o mesmo, excepto que os valores representados por cada dígito são calculados através de potências de 2, pois o número de valores possíveis num dígito é 2. O valor máximo representado no primeiro dígito é 20, no segundo 21, no terceiro 23, etc..
A representação de números negativos coloca problemas em sistemas informáticos, pois os os valores possíveis de representar são binários, o que implica que o sinal "-" não esteja incluído. Daí ser necessário definir regras de representação.
A solução está em atribuir a um dos dígitos do número, informação acerca do sinal. Ou seja, definir um "bit de sinal". Se tal dígito estiver a 0 (zero) o valor será positivo, se estiver a 1 o valor será negativo. Por norma, o bit de sinal é o bit mais significativo do número. Esta representação denomina-se complemento para 1.
Número positivo: 001100
Número negativo: 1001100
No entanto isto levanta um questão interessante: e o zero, também pode ser negativo? Se considerarmos que o número é representado pelo computador usando 4 bits, teríamos:
7 6 5 4 3 2 1 0 -0 -1 -2 -3 -4 -5 -6 -7 |
0111 0110 0101 0100 0011 0010 0001 0000 1000 1001 1010 1011 1100 1101 1110 1111 |
Portanto, para além de ser incorrecto representar-se o valor -0, existe uma combinação de dígitos que poderia ser usada para um outro valor válido.
A solução está em usar a representação em complemento para 2. O complemento para 2 dum número encontra-se usando o seguinte algoritmo:
5 = 0101 -complemento-> 1010
+ 1
-----
1011 = -5
Assim a representação em complemento para 2, e que é a representação corrente em informática, será:
7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 -6 -7 -8 |
0111 0110 0101 0100 0011 0010 0001 0000 1111 1110 1101 1100 1011 1010 1001 1000 |
Ou seja, existe mais um valor negativo que anteriormente, e que substitui o
-0.
Aplica-se o mesmo procedimento quer se trate de 4, 8, 16, 32 ou outro qualquer
número de bits.
Conversão aritmética de números significa a tradução da representação de
determinado número duma determinada notação para outra, sem que o valor real do valor
se altere.
No sentido de se identificar os procedimentos de conversão entre bases, analisa-se de
seguida os procedimentos considerando a base decimal como destino e origem dos números.
Assim, identificam-se dois tipos de procedimentos:
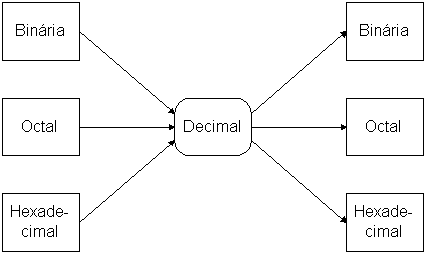
Figura 4 - Conversão de e para base decimal
A conversão de um número de uma outra base para base decimal, utiliza-se a ponderação dos pesos dos dígitos do número.
101(2) = 1*20+0*21+1*22 = 1*1+0*2+1*4 = 6(10)
34F7(16) = 7*160+F*161+4*162+3*163 = 7*1+15*16+4*256+3*4096 = 13559(10)
Qualquer valor pode ser convertido para outra base através de divisões sucessivas pelo número representativo da base para a qual se deseja converter. O número convertido encontra-se pelo agrupamento dos dígitos do resto. Este procedimento corresponde à separação das várias parcelas componentes do número (cada dígito representa determinado valor absoluto).
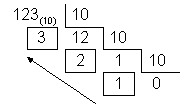
O valor 123(10) corresponde na base decimal a 123(10). |
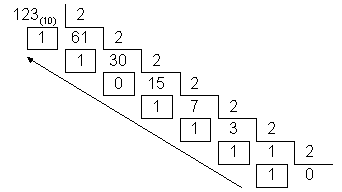 O valor 123(10) é representado na base binária por: 1111011(2). |
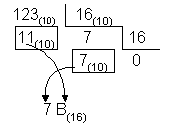
O valor 123(10) é representado na base hexadecimal por: 7B(16). |
Este procedimento parte do pressuposto e do conhecimento da tabuada da base do número a converter. Ou seja, se o número estiver numa base X, processo terá de utilizar a tabuada da base X, o que convenhamos é complicado pois a tabuada que se aprende (e decora) é a tabuada na base decimal.
O valor 123(8) é representado na base binária por: 1010011(2) |
O valor 1101(2) é representado na base decimal por: 13(10) |
273(8) = 3*80+7*81+2*82 = 3*1+7*8+2*40 = 3+38+80 = BB(16)
1101(2) = 1*20+0*21+1*22+1*23 = 1*1+0*2+1*4+1*10 = 1+0+4+10 = 15(8)
Não é prático converter um número duma base que não a decimal, para outra base. No entanto observa-se que:
- Existem determinadas bases numéricas, que tem a particularidade do seu dígito mais elevado usar um número fixo de dígitos binários completamente ocupados, ou seja, todos a 1. Por exemplo, 3(4) = 11(2), 7(8) = 111(2), ou F(16)=1111(2).
Assim, uma cadeia de dígitos binários pode ser subdividida em grupos de dígitos. A partir daí bastará fazer corresponder a cada grupo de dígitos binários o dígito na base específica. Assim, conhecendo apenas um conjunto limitado (e simples) de relações entre números em diferentes bases (ver Tabela 1), é fácil e imediato fazer conversões.
Binário - Octal |
Binário - Hexadecimal |
111 110 100 100 110(2) = 7 6 4 4 6(8) Conversão entre base binária e octal por agrupamento 3 a 3 de dígitos binários. |
111 1101 0010 0110(2) = 7 D 2 6(16) Conversão entre base binária e octal por agrupamento 4 a 4 de dígitos binários. |
Usando os resultados das conversões de binário para octal ou hexadecimal, também o procedimento de conversão de binário para decimal se torna menos exaustivo, uma vez que se pode usar o valor em octal ou hexadecimal para a conversão.
| Binário - Octal | Binário - Hexadecimal | Binário - Decimal |
101 111 011(2) = 5 7 3(8) |
1 0111 1011(2) = 1 7 B(16) |
101111011(2) = 573(8)= 3*80+7*81+5*82 = 379(10) |
Converter o número 761(8) para base binária, hexadecimal e decimal.
| Octal - Binário | Octal - Hexadecimal | Octal - Decimal |
7 6 1(8) = 111 110 001(2) |
761(8) = 1 1111 0001(2) 1 F 1(16) |
761(8) = 1*80+6*81+7*82 = 497(10) |
As operações aritméticas, seguem os mesmos procedimentos seja qual for a base numérica em questão. No entanto analisa-se de seguida os procedimentos aplicados nas operações:
Nota: Os valores a vermelho por cima dos operadores, representa o "que vai" ou em terminologia informática o "carry".
| Decimal | Binária | Octal | Hexadecimal |
1 9 + 1 ----- 10 |
1 1 + 1 ----- 10 |
1 7 + 1 ----- 10 |
1 F + 1 ----- 10 |
11 1292 + 873 ------ 2165 |
111
101
+ 10111
--------
11100
|
11 67 + 32 ----- 121 |
1 4F12 + 9F ----- 4FB1 |
| Decimal | Binária | Octal | Hexadecimal |
1 12 - 5 ----- 07 |
1 10 - 1 ----- 01 |
1 12 - 5 ----- 05 |
1 1B - C ----- 0F |
1 5 - 12 ----- - 07 |
11 110 - 1001 -------- - 0011 |
11 56 - 302 ------ - 224 |
1 4F2 - DA9F ------- - D5AD |
Os procedimentos relativos à operação de multiplicação são os mesmo qualquer que seja a base numérica, mas como já havia sido referido, a tabuada que se conhece é a tabuada decimal, pelo que não é simples realizar as operações de multiplicação e divisão.
| Decimal | Binária | Octal | Hexadecimal |
1 12 * 5 ----- 60 |
10 * 1 ----- 10 |
1 12 - 5 ----- 62 |
2 1B - 3 ----- 51 |
O mesmo princípio se aplica para a operação divisão, uma vez que o algoritmo se baseia na tabuada.
A álgebra de Boole deve o seu nome ao matemático inglês George Boole (1815-64), pela sua contribuição para a lógica simbólica. Boole defendeu que a lógica deveria ser aliada à matemática e não à filosofia, como até então era habitual.
Boole desenvolveu várias regras e propriedades da lógica simbólica como a propriedade associativa, propriedade distributiva, propriedade associativa. No entanto, analisaremos apenas:
Operações booleanas são operações realizadas sobre valores (operandos) binários. Ou seja, operandos que tomam apenas dois valores mutuamente complementares, por exemplo Verdadeiro/Falso, 0/1, Existente/Inexistente.
Existem 4 operações lógicas binárias simples através das quais se constróem sistemas lógicos complexos:
A operação booleana Ou (Or) é representada pelos símbolos ![]() ,
. e * e em terminologia informática pelo operador and.
,
. e * e em terminologia informática pelo operador and.
Tem 2 operandos e caracteriza-se pelas seguintes relações:
| a | b | and |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Só se as duas condições (preposições) a e b forem simultaneamente 1 (verdadeiras) é que o resultado é 1 (verdadeiro).
A operação booleana Ou (Or) é representada pelos símbolos ![]() e + e em terminologia informática pelo operador or.
e + e em terminologia informática pelo operador or.
Tem 2 operandos e caracteriza-se pelas seguintes relações:
| a | b | or |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Basta que uma das (preposições) a ou b seja 1 (verdadeira) para que o resultado seja 1 (verdadeiro).
A operação booleana XOu (XOr) é representada pelos símbolos ![]() e
e ![]() e em terminologia
informática pelo operador xor.
e em terminologia
informática pelo operador xor.
Tem 2 operandos e caracteriza-se pelas seguintes relações:
| a | b | xor |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
O resultado é 1 (verdadeiro) se apenas uma das preposições a ou b for 1 (verdadeira).
A operação booleana Complemento (Not) é representada pelos símbolos -
(coloca-se antes do operando) e ![]() (coloca-se sobre o operando), e em terminologia informática pelo operador not.
(coloca-se sobre o operando), e em terminologia informática pelo operador not.
Tem 1 operando e caracteriza-se pelas seguintes relações:
| a | not |
|
0 |
1 |
|
1 |
0 |
O resultado é o complemento do valor do operando.
Existem várias aplicações para lógica binária, mas provavelmente a que mais
se utiliza está relacionada com a representação de informação binária.
Isto é, informação que apenas tem dois estados.
Por exemplo, uma janela em Windows caracteriza-se tipicamente por ter ou não
determinados elementos:
Existirá porventura um estrutura interna do Windows que terá esta informação. Será razoável que para cada um destes elementos se use um Byte (char)? Um byte tem 8 bits e cada um pode representar os (tais) dois estados que são necessários. Ou seja, posso representar 8 elementos com um só byte. Por isso, usar um byte para representar apenas um valor binário é um desperdício de espaço.
Assim, o que se faz é usar estruturas (numéricas) como o byte, o char ou int, e a cada bit é atribuído um significado.
| Scroll bar | States | Buttons | Menu | Frame | Title |
Figura 7 - Um byte representando várias valores binários
Estas estruturas serão daqui em diante tratadas como conjunto de
estados binários.
No entanto não é comum as linguagens de programação terem instruções de
teste a bits específicos, e mesmo que os tenham, como é que tal é
internamente executado?
Para isso usa-se o conceito de máscara. Uma máscara é composta por:
O valor que contém os elementos a testar. O seu conteúdo é desconhecido;
Um valor que servirá de filtro, do mesmo tamanho que o anterior e que combinado com o operador deixará passar apenas os valores desejados;
Um operador booleano com o qual o valor e o filtro serão combinados.
Imagine-se que o objectivo é saber se determinada janela tem barra de estados. Sabe-se de antemão que a informação sobre esse elemento está no bit 5 (conta-se a partir do 0). Assim, o que se tem a fazer é encontrar um filtro e um operador que em combinação criem apenas dois resultados possíveis. Ou seja, com o bit 5 a 1 ou a 0 e todos outros iguais (seja 1 ou 0).
Valor dos elementos: ? ? ? ? ? ? ? ?
Máscara (Filtro + Operador): or 1 1 0 1 1 1 1 1
--------------------
Resultado: 1 1 ? 1 1 1 1 1
Os resultados possíveis são:
Valor dos elementos: ? ? ? ? ? ? ? ?
Máscara (Filtro + Operador): or 0 0 1 0 0 0 0 0
--------------------
Resultado: 0 0 ? 0 0 0 0 0
Os resultados possíveis são:
Para o caso "da scroll bar", e se se usasse a rotina de máscara descrita no exemplo1, a rotina de teste deveria ser semelhante ao seguinte código (em C):
#define(EXIST_SCROLL_BAR,255); char elements, mask_result;elements=what_elements(); mask_result=mask_or(A);if (mask_result==EXIST_SCROLL_BAR) printf("Tem scroll bar."); else printf("Não tem scroll bar.");
Existem em informática duas operações sobre valores numéricos que merecem ser apresentadas, mas que não encaixam completamente no conceito de aritmética embora permitam realizar determinadas operações aritméticas, mas também não são operações booleanas, embora permitam realizar algumas tarefas sobre bits semelhantes a máscaras. Estas duas operações são:
Existem várias variantes desta operação, pelo que se apresenta a mais
genérica.
Deslocamento, em inglês e terminologia informática, Shift, faz deslocar todos
os bits duma estrutura para a direita ou para a esquerda, conforme seja uma
Deslocação para a direita ou para a esquerda. Se se deslocam, o bit que está
na extremidade (direita ou esquerda conforme o movimento) é expulso, enquanto
que do lado oposto tem de entrar um valor, normalmente 0 (zero).
![]()
Figura 8 - Representação de deslocamento para a esquerda
As aplicações lógicas e teste de bits são possíveis pois o número é expulso para um local que, por norma se denomina Carry Flag (CF) e que, este sim, pode ser testado com uma instrução semelhante a:
if (CF==1) goto lineX; else goto lineY;
Assim, é possível com deslocamentos sucessivos testar qualquer um dos bits. No entanto, como o valor do bit é expulso, não é possível através da operação em sentido contrário repor o valor anterior, pelo que o valor (se não for guardado previamente) é perdido.
Quanto a aplicações aritméticas, estas resumem-se à aplicação de
princípios óbvios. Observe-se.
Quando se deseja multiplicar um número decimal por 10, 100, 1000, enfim
potências de 10, não é necessário recorrer ao algoritmo comum para outros
valores. O que se faz é simplesmente acrescentar um 0 (zero) à direita do
número. Ou seja, fazer um deslocamento para a esquerda.
O mesmo procedimento pode ser aplicado em número binários, sendo que a
multiplicação não é por potências de 10 mas sim por potências de 2. Assim,
um deslocamento de 4 posições corresponde a fazer uma multiplicação de 24=16.
Deslocamentos para a direita têm o efeito contrário, ou seja divisão.
Estas formas de multiplicar e dividir têm a vantagem de ser substancialmente mais rápidas que a multiplicação e divisão tradicionais, o que acontece
também em computador (mais correctamente no CPU).
Existem várias variantes desta operação, pelo que se apresenta a mais
genérica.
Rotação, em inglês e terminologia informática, Rotate, faz rodar todos os
bits duma estrutura para a direita ou para a esquerda, conforme seja uma
Rotação para a direita ou para a esquerda. Se rodam, o bit que está na
extremidade (direita ou esquerda conforme o movimento) é expulso, mas entra na
extremidade oposta.

Figura 9 - Representação de rotação para a esquerda
Normalmente o número é expulso para um local que se denomina CF (Carry Flag) e que, este sim pode ser testado com uma instrução semelhante a:
if (CF==1) goto lineX; else goto lineY;
Assim, é possível com rotações sucessivas testar qualquer um dos bits, sem que o problema descrito para o deslocamento ocorra, pois os bits são simultaneamente expulsos e integrados na estrutura na outra extremidade. A rotação em sentido contrário e no mesmo número de vezes da anterior repõe o valor original.
| Bit menos/mais significativo | O adjectivo "significativo" respeita
ao valor que o dígito representa (ou bit) no número, ou seja o peso do
dígito. Na base decimal, cada dígito tem um nome: unidades, dezenas,
centenas, milhares, etc. O dígito menos significativo dum número decimal
inteiro é as unidades. Assim, a "significância" dos dígitos (ou bit) no número aumenta da direita para esquerda. O bit menos significativo é à direita, enquanto o mais significativo é o que está mais à esquerda. |
| MSB/LSB | (Most/Less Significatif Bit) ver bit menos/mais significativo |
| Nibble | Grupo de quatro bits. Num byte existe o nibble mais e menos significativo, seguindo o princípio de bit menos/mais significativo. |
É objectivo deste estudo:
Última actualização: 02 Maio 2005